Fabien Marche - software
Ma binette

WaveBox

WaveBox is a multi-models numerical platform written in C++ dedicated to the approximations of the solutions of several shallow water asymptotics in the surface dimension d=2 with efficient combined Hybridized Discontinuous Galerkin (HDG) and DG methods on general unstructured meshes (Saint-Venant, Boussinesq and Green-Naghdi equations equations). Main features:

    sub-models CPU-GPU co-processing
    arbitrary order of accuracy (h and p-adaptivity)
    robust treatment of the run-up and flooding processes (strict maximum-principle enforcement)
    well-balancing for motionless steady states
    unstructured meshes
    wave breaking treatment with dynamic switching strategy

GN2D (not maintained anymore)

GN2D is a numerical resolution code for the 2D Green-Naghdi (or fully non-linear Boussinesq)) equations, relying on a hybrid Finite-Volumes/Finite-Differences discretization. The main features are

    High-order accuracy in space: WENO reconstructions up to 5th order
    Robust treament of the run-up and flooding processes
    Well-balancing
    Handles cartesian structured meshes
    Handles waves breaking with a dissipation-based switching strategy (developped during M. Tissier Ph.D. thesis.)

Main publications associated with GN2D:

  • P.Bonneton, F. Chazel, D.Lannes, F.Marche, M.Tissier [journal]
    A splitting approach for the fully nonlinear and weakly dispersive Green-Naghdi model.
    J. Comput. Phys., volume 230(4), pages 1479 - 1498, 2011.
  • F. Chazel, D.Lannes, F.Marche. [journal]
    Numerical simulation of strongly nonlinear and dispersive waves using a Green-Naghdi model.
    J. Sci. Comput., volume 48(3), pages 105-116, 2011.
  • M.Tissier, P.Bonneton, F.Marche, F.Chazel, D.Lannes [journal]
    A new approach to handle wave breaking in fully non-linear Boussinesq models.
    Coastal Engineering, volume 67, pages 54--66, 2012.
  • D.Lannes, F.Marche [HAL]
    A new class of fully nonlinear and weakly dispersive Green-Naghdi models for efficient 2D simulations.

    • SURF-WB (not maintained anymore)

    SURF-WB is a numerical code for the approximations of the Saint-Venant 2DH equations' weak solutions, relying on a Finite-Volume approach. Its main features are:

      High order accuracy in space: MUSCL and WENO reconstructions, up to 5th order on structured meshes and 2nd order on unstructured meshes
      MPI parallelisation
      Robust treatment of flooding and run-up
      Well-balancing: steady states are preserved
      Handles cartesian, triangular unstructured and curvi-linear meshes (the later developped in a joined work with M.Guerra, R. Cienfuegos, C.Escauriaza, J.Galaz)
      Able to simulate simultaneously wave overtopping and the resulting flood in an urban area at a very high resolution (joined work with Le Roy S., Pedreros R., André C., Paris F., Lecacheux S. and Vinchon C., BRGM, see picture above and beside)

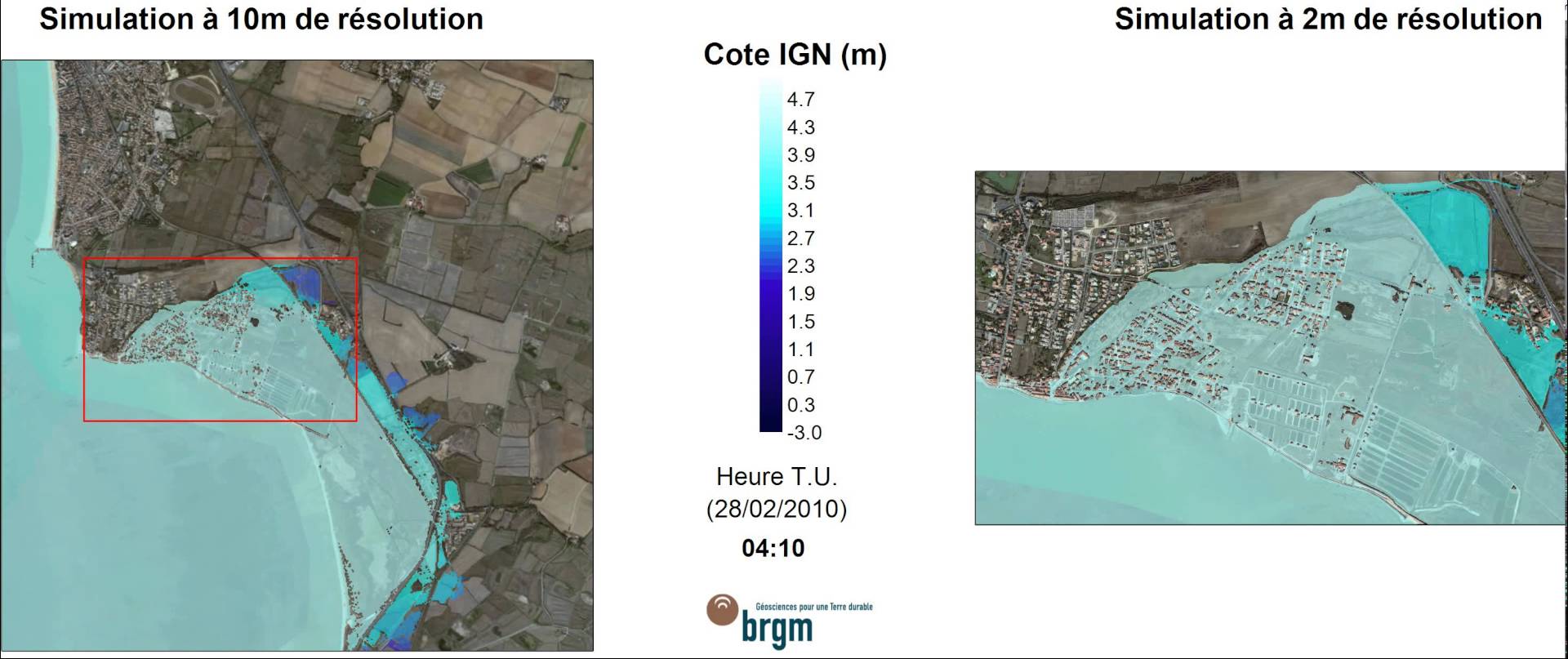    This code has been extensively used by several institutes (BRGM -Unité Risques Côtiers et Changements Climatiques-, Hydraulic and Environmental Engineering Department, Pontificia Universidad Catolica de Chile, LEGI Grenoble, EPOC Bordeaux) and for several projects (ANR MISSEVA, ANR MathOcean, ECOS-CONYCIT, JOHANNA, SUBMERSION, ...).

    The picture above is issued from a simulation of the submersion in Les Bouchôleurs (17, France) (where I grew up ...) during storm Xynthia, 2010 (joined work with Le Roy S., Pedreros R., André C., Paris F., Lecacheux S. and Vinchon C.)


    Here are examples of computations performed with SURF-WB:
    Animation Gâvres 1 (Visualisation Submersion Urbaine-3D, Ministère de l’Ecologie)
    Animation Gâvres 2 (JOHANNA project - BRGM and Fondation MAIF)
    Animation Yves et Chatelaillon (SUBMERSION project - BRGM)


    Main publications associated with SURF-WB:
  • F. Marche, P. Bonneton, P. Fabrie, N. Seguin [journal]
    Evaluation of well-balanced bore-capturing schemes for 2D wetting and drying processes.
    International Journal for Numerical Methods in Fluids, volume 53(5), pages 867-894, 2007.
  • C.Berthon, F.Marche [journal]
    A positive preserving high order VFRoe scheme for shallow water equations: a class of relaxation schemes.
    SIAM J. Sci. Comput., volume 30(5), pages 2587-2612, 2008.
  • Q.Liang, F.Marche [journal]
    Numerical resolution of well-balanced shallow water equations with complex source terms.
    Adv. Water Res., volume 32(6), pages 873-884, 2009.
  • C.Berthon, F.Marche, R.Turpault [journal]
    An efficient scheme on wet/dry transitions for shallow water equations with friction.
    Computers & Fluids, volume 48(1), pages 192 - 201, 2011.
  • A.Duran, Q.Liang, F.Marche [journal]
    On the well-balanced numerical discretization of shallow water equations on unstructured meshes.
    J. Comput. Phys., volume 235, pages 565--586, 2013.
  • S.Le Roy, R.Pedreros, C.André, F.Paris, S.Lecacheux, F.Marche,C.Vinchon [journal]
    Coastal flooding of urban areas by overtopping: dynamic modelling application to the Johanna storm (2008) in Gâvres (France).
    Natural Hazards and Earth System Sciences, volume 15, pages 2497-2510, 2015.
    • LJLL UPMC     CNRS CNRS