Sample menu:
Research activites
My research activity at Montpellier is now mainly focused on computational cardiovascular biomechanics; the developments made within the group I am leading are gathered in the YALES2BIO solver for the description of blood flows at both micro and macro scales. I am also still working in close connection with CERFACS , addressing issues related to combustion noise, thermo-acoustic instabilities and wall modeling. Some examples of recent realizations I was involved in are given below. This is not an exhaustive list; refer to my publications and/or PhD students to obtain a more complete view of my research activities.
Subgrid scale modeling for LES
The WALE model (Nicoud and Ducros, Flow Turb. and Comb., 62(3), 1999) is now recognized as a simple yet efficient way to represent the effect of subgrid scales in wall bounded turbulent flows in complex geometries. However, a careful examination of the underlying spatial operator demonstrates that this model overestimates the eddy-viscosity and thus subgrid scale dissipation in some academical flows (e.g.: 2D vortex). This motivated the design of the so-called Sigma model (Nicoud et al., Phys. Fluids, 23(8), 2011) which has the unique property to vanish as soon as the resolved field is either two-dimensional or two-component, including the pure shear and solid rotation cases. As the WALE model, it also has the appropriate cubic behavior in the vicinity of solid boundaries without requiring any ad-hoc treatment. This model proved more accurate that the dynamic Smagorinsky model in several cases, including the pulsatile hot jet experiment developed at IFPEN during Hubert Baya Toda's thesis.
(Baya Toda et al., Phys. Fluids, 26, 2014)
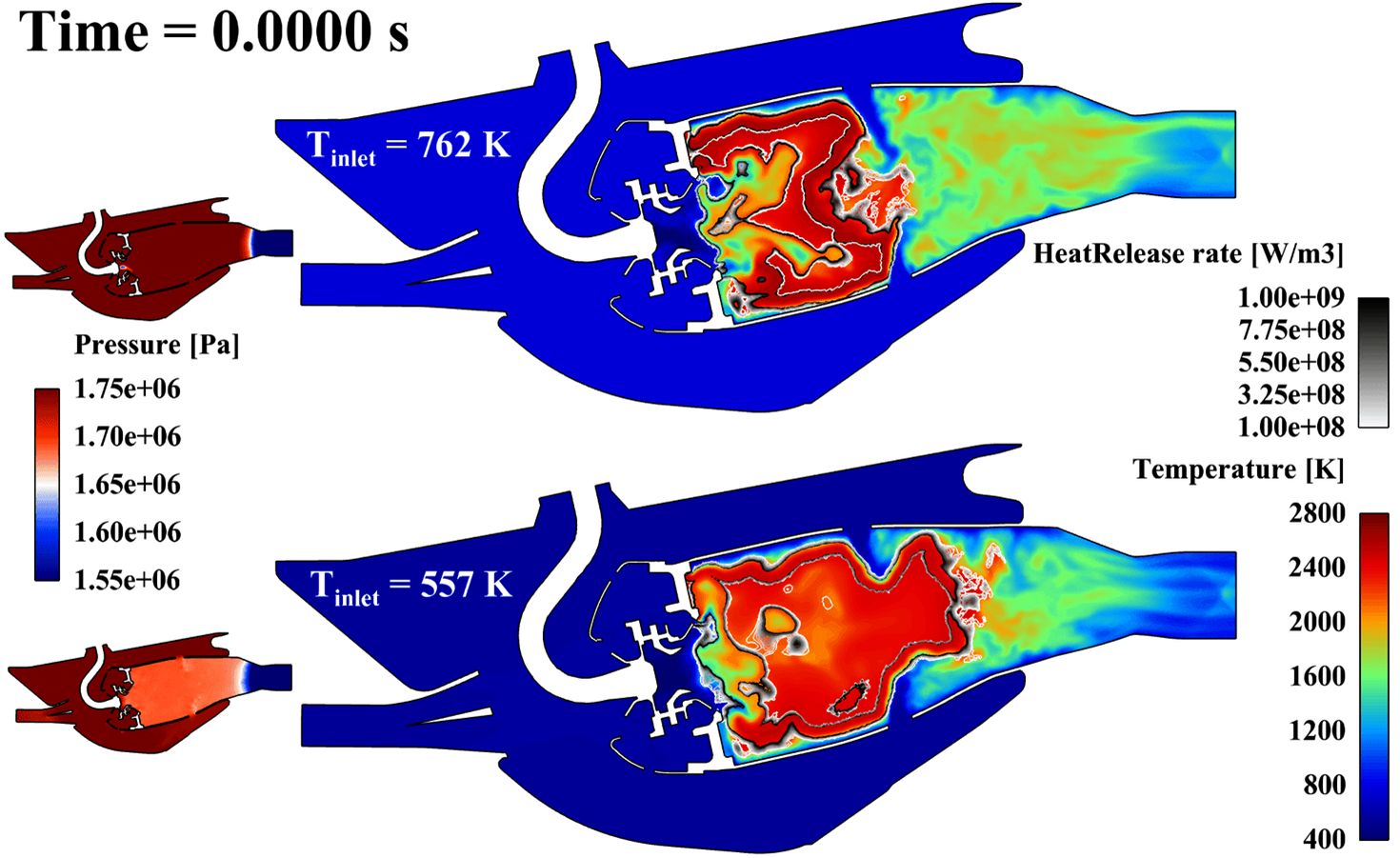
Entropy-acoustic coupling in a realistic aeroengine
Thermoacoustic instabilities are frequently encountered during the development of low pollutant emissions combustors. While Large-Eddy Simulation is now accepted as a very powerful tool to numerically reproduce these instabilities, it also proves useful to use low order models to better understand the nature of these instabilities. The AVSP solver (Nicoud et al., AIAA J., 45(2), 2007) solves the Helmholtz equation for the acoustic pressure over a non-isothermal flow in complex 3D domains bounded by arbitrary boundary impedances. Fed with appropriate data for the flame response to acoustic excitations, this approach proved efficient to reproduce the stability map of several academic (e.g.: Silva et al., Comb. Flame, 160(9), 2013) and industrial (e.g.: Selle et al., Comb. and Flame, 145, 2006) combustors, including annular chambers with multiple burners (Sensiau et al. Int. J. Aeroacoustics, 8(1), 2009) without or with multiperforated liners (Gullaud and Nicoud, AIAA J., 50(12), 2012). The Helmholtz equation relies on the so-called zero Mach number assumption stating that the mean velocity is very small compared to the speed of sound. A recent study suggests that the domain of validity of the zero mean flow assumption might be rather small (Nicoud and Wieczorek, Int. J. Spray Comb. Dyn., 1(1), 2009). One reason for this is that this equation does not support entropy waves, preventing the acoustic generation due to the entropy spots being accelerated in the dowstream nozzle to be accounted for. A Delayed Entropy Coupled Boundary Condition was recently introduced to correct this drawback of the Helmholtz approach (Motheau et al., J. Sound and Vibration, 2013) and successfully applied to an actual SAFRAN aeroengine (Motheau et al., J. Fluid Mechanics, 749, 2014). All the features developed over the year are now beeing integrated in another numerical framework based on the use of frames and state-space representations to speed up (x100) the modes computation compared to the Helmholtz strategy. The foundations of this divide-and-conquer strategy are detailed in Laurent et al., Comb & Flame, 206, 2019 and Laurent et al. JCP, 428, 2021
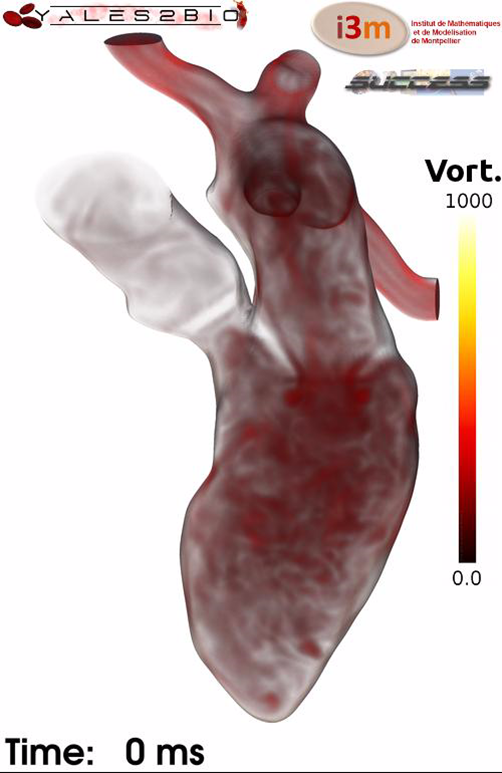
Cardiac turbulence
The hemodynamics within a human left heart was computed thanks to the YALES2BIO solver used together with the Medical Imaging-CFD framework developed within the OCFIA research program and successfully applied to large vessels (Midulla et al., Eur. Radiol, 22(10), 2012). Ten ECG gated CT images were acquired along the cardiac cycle and used to generate a 3D finite volume mesh evolving consistently with the observed geometry changes. The Arbitrary Lagrangian Eulerian methodology was then used to solve the Navier-Stokes equations within the computational domain which contains the four pulmonary veins, the left atrium and ventricle and the ascending aorta. The mitral and aortic valves were accounted for thanks to a simplified Immersed Boundary Method. A multi-cycle Large-Eddy Simulation allowed to clearly establish the turbulent nature of the intra cardiac flow during certain phases of the cycle (Chnafa, Mendez and Nicoud, Comp. Fluids, 94, 2014). The same methodology was applied to a normal heart by using MRI data as detailed in Chnafa, Mendez and Nicoud, ABME, 2016. The intracardiac flow numerical database is now being used in the development an automatic method for reconstructing 2D/3D velocity vector fields within the left ventricular cavity from single-view color Doppler echocardiographic images (Assi et al., PMB, 62, 2017; Vixege et al., PMD, 66, 2021; Vixege et al., PMD, 67, 2022).
(from C. Chnafa, IMAG)
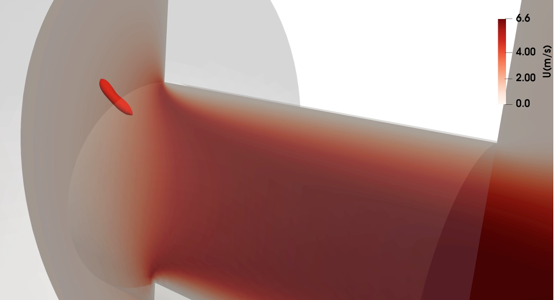
Small scales Blood flows
The YALES2BIO solver is also used in order to describe the dynamics of red blood cells in microfluidics. An immersed boundary method is used to model the fluid-structure interaction between the membrane and the inner/outer fluids (Mendez, Gibaud and Nicoud, JCP, 2014). The methodology was validated in several cases including the damped oscillations of a capsule (Martins Afonso, Mendez and Nicoud, JFM, 2014), the stretching of a capsule in a linear shear flow or of a red blood cell in an optical tweezers experiment (Siguenza et al., JCP, 2016). The YALES2BIO simulations allow to retrieve the red blood cell dynamics observed experimentally by Lanotte et al., PNAS, 2016, including the trilobed shape at large shear rate (Mauer et al., PRL, 2018). The main industrial application is in collaboration with the Horiba Medical company and deals with the study of the counting and sizing of the red blood cells within the Coulter-based cytometers. A major outcome of the numerical pipeline developed at IMAG (Taraconat et al., IJNMBE, 2019) is the understanding of the dynamics of the red blood cells when they flow throughout the device (Taraconat et al., Cytometry, 2021) and its consequences in terms of volume assessment (two patents).
(from P. Taraconat, IMAG)
Multiphysics simulations
Several situations computed thanks to the YALES2BIO solver involve not only hemodynamics but also its coupling with another physical mechanism. The natural coupling is with solid mechanics and the Immersed Boundary Methods developped to reproduce the dynamics of red blood cells can be used to this regards. For example, the motion of a biomimetic artic valve manufactured and studied experimentaly at the Helmholtz institute of Aachen (Germany) was succeffuly reproduced (Siguenza et al., IJNMBE, 34, 2018). Fluid mechanics may also be coupled to biochemistry in order to represent thrombosis and coagulation. In Rojano Mendez et al. BMM, 17, (2018), a proper modeling of the contact system initiated by the adsoprtion and auto-activation of Factor XII was developed and successfully applied to a backward facing step experimental setup studied at Penn State. Another coupling is with the Block equations for the evolution of the magnetization field induced by isochromat while they are transported by the flow. The pipeline developed in the group in collaboration with the Spin Up company allows to generate 4D flow MRI images in silico (Puiseux et al., PLOS One, 16, 2021). This technology is a first step towards a better understanding of the measurement errors when using adbanced imaging technics in clinics (one patent).
(from J. Siguenza, IMAG)